- The output should contain x, y, and INSTRUMENTAL v magnitude corresponding to SOME frame you love, preferably with good seeing. This will be used to determine the offsets (angle, x, y, and magnitude) from one frame to another.
- It should contain the RA and DECs of each star referenced to the appropriate coordinate system (GSC in this case).
- It should contain the STANDARD V magnitude and colors for all the stars. These should be derived from the data themselves once the color terms are known.
- It should contain the spectral types, cross-IDs and other photometry when available.
Here's how I did it...
- FOR THE SWOPE DATA:
- Picked out a nice set of 6 V's, 6 U's, 6 B's, and 6 R's. Stuck them in their own little subdirectory.
- Ran the automatic photometry routine "autoswope" on these.
- Put the V output files ("sum's") into allfiles
- copied one of these to MasterList. In the case of NGC346 this is n16ccd069.
- ran matchxy3 [for Swope] (see below) [creates "allshifts"]
- ran combine [creates fort.3] using the data in "allshifts"
- Get rid of the single detections:
- sort fort.3 col=5 num+ > temp1
- Edit out the single detections, and then sort by magnitude:
- sort temp1 col=3 num+ > vxy.dat
- Get rid of close matches: Ran filter [vxy.dat--->fort.3]
- Get rid of faint things: Edited fort.3 to get rid of 22.000+ ---> vxyed.dat
- Display and make sure you're happy.
- Create ra and dec file:
- tfinder on the master image
- wsctran vxyed.dat vrd.dat %12.2H %12.1h
- Note: For the R136 images there were only 3 stars that showed up.
The solution was awful when I ran it with the schmidt catalog. So, I did
a very painful thing and used astrom to determine the answers.
Then I edited them into the header as follows:
- X=a+b*XMEAS +c *YMEAS; Y=d+e*YMEAS + f*XMEAS [from astrom]
- CD1_1 = c ---> degrees
- CD1_2 = d ---> degrees
- CD2_1 = f(!)---> degrees
- CD2_2 = e(!) ---> degrees
- Fiddled with zero points by putting in XMEAS zeropoint as CRPIX1, but explictly then computing the RA that went to that and putting that in as CRVAL1 in degrees.
- Note: Remind me some day to write a routine that does this automatically. Sheesh.
- Note: For the R136 images there were only 3 stars that showed up.
The solution was awful when I ran it with the schmidt catalog. So, I did
a very painful thing and used astrom to determine the answers.
Then I edited them into the header as follows:
- Add color information:
For B, R, and U did the following:
- put a set in "allfiles"
- select a master file (usually the first long exposure)
- Anymatchxy (same as "matchxy", but ignores the filter...)
- combine , then cp fort.3 uxy.dat
- tfinder on master image
- wcsctran uxy.dat--->urd.dat
When done with all filters, ran "color" and captured the output as "vubr.dat" Note that if you only have two filters (B and V, say) this still works.
-
Now calibrate these....
- Use "dumpem" to dump the SMC catalog --->00 59 04.7 -72 10 266. 2000. Search radius 1000.
- mv fort.3 sch.cat
- Run ../calibrate
This produces files fort.7-10, which we can then fit using "curfit" in IRAF.
Suggest using curfit with nit=10, high=2.5, low=2.5
fort.7: B-V, vi-v, d fort.8: U-B, ui-u, d fort.9: B-V, bi-b, d fort.10: V-R, ri-r, d MASSEY ET AL 1989 v-V=3.616-0.252(B-V) rms=0.05 u-U=5.958-0.249(U-B) rms=0.05 b-B=4.423-0.114(B-V) rms=0.05 Schmidt data to only the instrumental < 19. FINAL: v-V=3.747 -0.05(B-V) rms 0.05 mag vs 3.616 0.13 u-U=6.155 -0.21(U-B) rms 0.08 mag vs 5.958 0.20 b-B-4.513 -0.08(B-V) rms 0.07 mag vs 4.423 0.09 r-R=3.707 -0.04(V-R) rms 0.06 mag For N602c, did NOT restrict the magnitude range and still got rms of 0.03! When we did restrict it it did get cleaner, but no real difference in vals v-V=3.620-0.077(B-V) rms0.04 mag u-U=6.157-0.161(U-B) rms 0.05 mag b-B=4.156-0.074(B-V) rms 0.04 mag r-R=3.558-0.011(V-R) rms 0.06 mag For R136, the solutions are Truely Lousy, with large rms... Helped once I brought the sky in: v-V=3.808-0.075(B-V) rms=0.09 b-B=3.827-0.103(B-V) rms=0.07 Very tempted to adopt "old" photometry when we can.... N1910: deleted >19 and then: v-V=3.683-0.074(B-V) rms 0.09 mag u-U=6.063-0.101(U-B) rms 0.10 mag b-B=3.821-0.058(B-V) rms 0.08 mag and editing out > 18.... r-R=3.399-0.041(V-R) rms 0.10 mag N6611: EXCELLENT FITS... v-V=3.480+0.071(B-V) rms 0.04 mag u-U=5.747-0.236(U-B) rms 0.06mag b-B=3.584-0.073(B-V) rms 0.05 mag
- Ran mkinvert to produce fort.22. This becomes the MasterList except that we don't have cross-IDs. Oh well!
- crossid02. Takes Masterlist and dumps to fort.3 (and the screen) the cross ids to the Massey (2002) catalog. It also puts a comparison of the magnitudes in fort.4.
- addtypesw addes in the spectral types from the SMC/LMC Schmidt catalog
- FOR THE SMARTS DATA....
- The problem for the SMARTS data is we never DID get B frames when
the seeing was reasonable: for instance, the best NGC 602 frames were with
7+ pixels FWHM. So, why not do this backwards? I started by finding
a night with good (but not great) images for all of the MC frames:
20051222. By coincidence, this happens to be the night I was sitting there
taking the data myself. What were the chances of THAT?
- NGC602
- Ran tfinder on Py051222.0059 (using !=04BU as the plate-id, i.e., 02I5 AND 06B1)
- wcsctran Py051222.0059sum ---> n602ml
- Ran matchsw to match the smarts instrumental magnitudes against the Swope MasterList. (fields fort.3 2,1 > fitxy) Found a great correlation with standard B-V; i.e., Vsmarts2-Vstd = 2.3449-0.17(B-V)std with an RMS of 0.03 mag. This included only the stars with v2error <0.05mag.
- Ran matchsw2 to apply the transformation and produce a file (n602ml2) with the RA, DEC, instrument mag + err, RA, DEC again, Vtransformed, B-V, U-B, and V-R (if in the Swope file), ID (if in the Swope file).
- Ran wcsctran to produce n602ml3. Almost the masterlist in the new "Smarts" format.
- Added in additional SMC stars using crosssm
- Final result was about 0.07 mag different in V than what is in the Schmidt catalog (on average).
- Added in additional spectral types using addtypes (operates on "MasterList" and creates fort.3)
- Let's try it out:
- files *sum > allfiles
- matchxy5
- starby5
- So, I compared the photometry of SMARTS vs Swope data for star W601 = O6.V in NGC 602: nominal V
mag of 15.19 vs 15.23. Here's the plot:
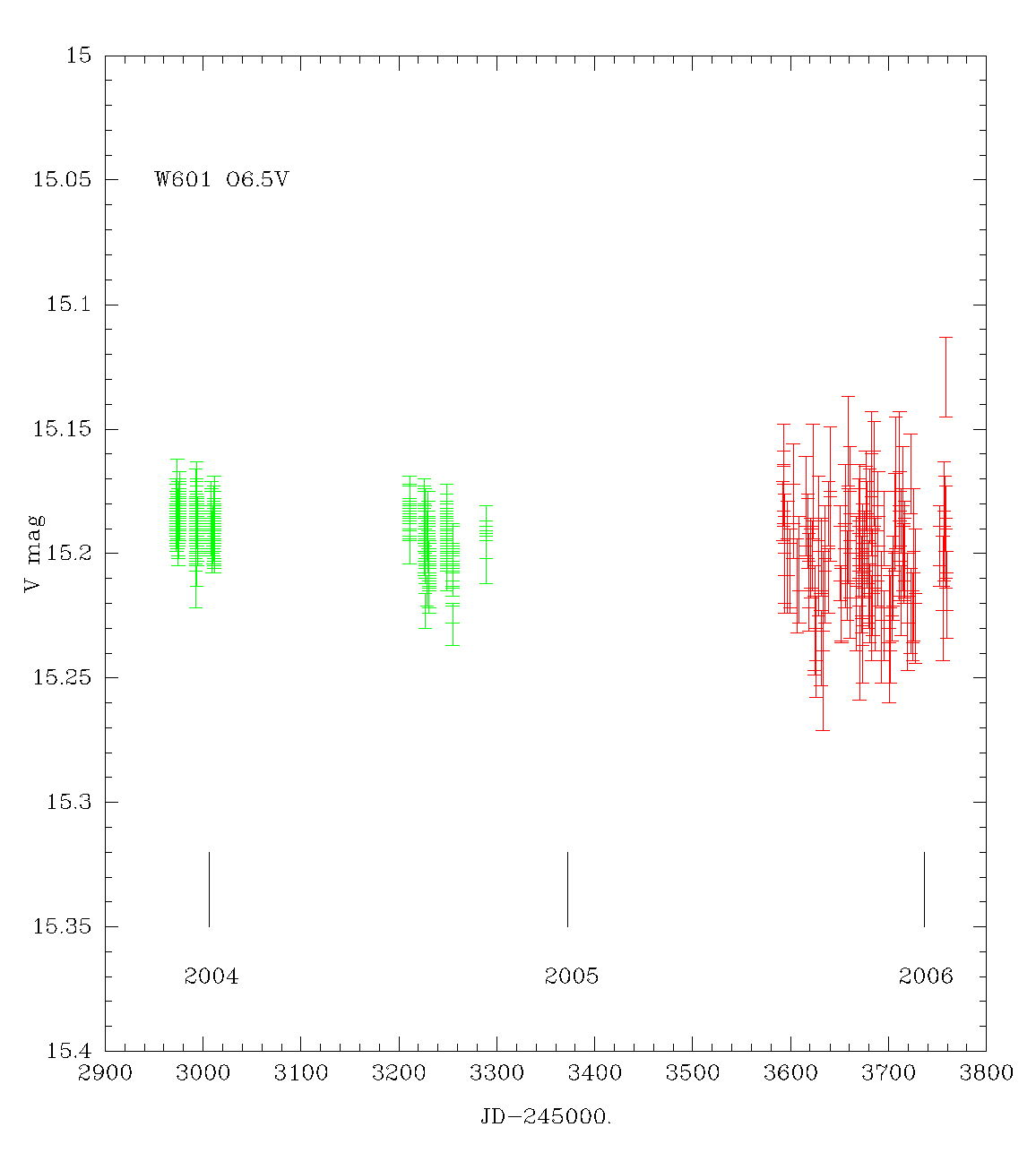
- NGC346:
- Used Py051222.0057
- Used same programs as above. Got Vsmarts-Vstd=2.532-0.146*(B-V), larger scatter (0.07 mag)
- Wound up arbitrarily changing the constant to 2.60 to make it agree better for the brighter stars. Don't know what the deal was.
- NGC1910=LH41
- Used Py051222.0061
- Used same programs as above. Got Vsmart-Vstd=2.53-0.207(B-V), scatter about 0.04. Looks great.
- NGC2044=LH90
- Used Py051222.0063, pinned it down with Br58.
- There were no Swope data for this cluster. Instead, there's photometry from three soucres: Testor et al (but no coordinates), the Liz paper (OK photometry), and the Schmidt images). For the Liz data (downloaded from Vizar), I wrote matchliz.f. Had to fudge the Liz coordinates a little: add 0.10 sec and -0.8" to liz. For these, we get: Vsmart-Vstd=2.525+0.01(B-V) with an RMS of 0.03 after killing a bunch of outlyers. There's not that many stars in the Liz catalog, so I did the same experiment with the Schmidt data (matchsch.f) data. Had gigantic scatter, but color relation seems very well determined: Vsmart-Vstd=2.56-0.08(B-V) with an RMS of 0.14. So, I am tempted to adopt Vsmart-Vstd=2.53-0.03(B-V) and let the chips fall where they may...
- Used crosssm as is to add in Schmidt stars
- Found a problem with the coordinates: had to add +0.10 time sec and -0.8 arcsec to the Liz coordinates to get them to match.
- NGC2074=LH101
- Used Py051222.0067
- Got GREAT solution (used Liz paper Lh101 and LH104 combined): Vsmart-Vstd=2.45 - 0.01(B-V) RMS of 0.01. Did the Schmidt as well: Vsmart-Vstd=2.63 - 0.12(B-V) RMS of 0.20. Gosh. Now what? Since we aren't combining these with anything, why not just use: Vsmart-Vstd=2.53 - 0.03(B-V), same as above, and call it even.
- More coordinates woes. Had to add -0.4 time sec to the Liz coordinates for LH101. Results for LH104 were more ambiguous.
- R136
- Used Py051222.0065
- Used "matchsw" programs. Got Vsmart-Vstd=2.58-0.152(B-V), scatter about 0.07. Looks great.
- But had to go back and add three stars by hand to MasterList:
very annoying, but they were near a bad column.
- So how did it work out? Here's the R136-007 light-curve, phased to 6.828 days:
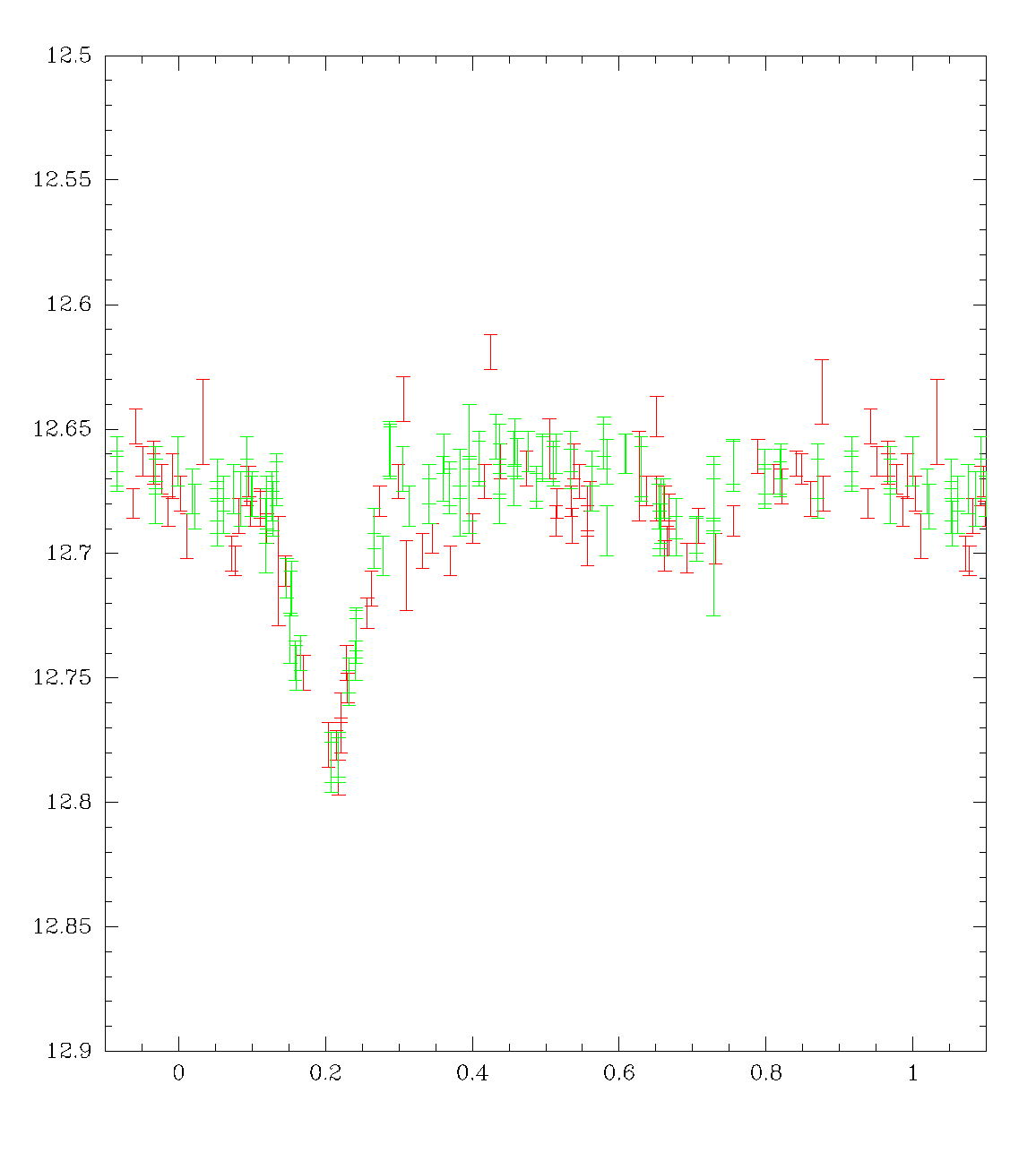
- So how did it work out? Here's the R136-007 light-curve, phased to 6.828 days:
- N3603
- Don't remember how we did it. Used Py060402.0072 as reference.
- Cl1715-387
- Hard to see why we bothered with 3 sec exposures; on the 10sec, the brightest star has peak counts of 18,000. (4.9 pixel FWHM). If the seeing got better than 3.5 pixels...OK, that makes sense. Anyway, used Py060402.0153 (one of the 10 sec exposures) as my reference.
- Solution was terrible, but sensible: Vsmarts-Vstd = 2.31 - 0.06(B-V). Used matchcl.f and then matchcl2.f
- Pismis24
- Used the 10sec Py060402.0157. Brightest star Pis24-1 was 28,000; FWHM=5.13. Used selectpars to limit the solution to 06Q3.
- Got nice solution: Vsmarts-Vstd=2.08-0.14 (B-V). Hmmm. Used it.
- Tr14 and Tr16
- Constructed a single cross-ID/photometry file called tr14.tsv, based upon a Vizar download of Table 4 from Massey & Johnson (1993), supplemented by Table 5 where I have turned the x's and y's into RAs and DECs.
- For Tr14, I used Py060402.0064 (0.3 sec) and came up with a solution Vsmarts=Vstd-2.14 + 0.02(B-V). Note the sign reversal.
- For Tr16, I used Py060402.0069 (68 was smeary, and I deleted it) and got 2.13+0.02(B-V). I suggest a compromise and use 2.135 and +0.06(B-V).
- NGC602
- The problem for the SMARTS data is we never DID get B frames when
the seeing was reasonable: for instance, the best NGC 602 frames were with
7+ pixels FWHM. So, why not do this backwards? I started by finding
a night with good (but not great) images for all of the MC frames:
20051222. By coincidence, this happens to be the night I was sitting there
taking the data myself. What were the chances of THAT?
- Now we use MasterList with each of the photometry files ("...sum")
to determine the offsets:
- cl files *sum>allfiles
- matchxy3. To some extent this is the real GUTS of the pipeline. It generates a single output file, "allshifts" (For the smarts data, I use "matchxy5.f")
- Now we use MasterList with each of the photometry files and the offset file "allshifts" to generate a star-by-star set of files containing JD and magnitudes... starby3. (For the smarts data, use starby5.)
- First, I moved things around. New structure:
- /Volumes/piglet/obins
- ["smarts" moved to /Volumes/Obinsresults on Jan 4, 2007]
- swope.
- clusters. I cut the old master lists at V=17.0.
The following contain the images and the photometry files:
- R136 MERGED
- n1910 MERGED
- n346 MERGED
- n602 MERGED
- n6611
- smarts
- clusters. The following contain the images and the photometry files:
- cl17
- n1910
- n2044
- n2074
- n346
- n3603
- n602
- pis24
- r136
- tr14
- tr16
- clusters. The following contain the images and the photometry files:
- results: For each star in each cluster should contain a single file, either merged, smarts, or swope.
- clusters. I cut the old master lists at V=17.0.
The following contain the images and the photometry files:
- So, I wrote "mergem.f" ("thinkem.f was the test case)
- swope.
- What about adding new data? We added in the next 6 months of Smarts
data, and it was pretty painless:
- cd /Volumes/Obinsresults/smarts/clusters/n346
- mkdir OLD
- mv N346sm* OLD/.
- scp panda:/smarts/massey/clusters/n346/Py06\* .
- load iraf
- delete allshifts,allfiles,allstars
- files P*sum > allfiles
- matchxy5
- delete all the 7999's, and the really rotten magnitude shifts
- starby5 (N346sm for the name)
- files N346sm* > allstars
- in "results", mkdir OLD, then mv N346* OLD/.
- edit /users/massey/survey/mergem.f to have the right cluster names
- mergem
- move on to the next cluster....
- Check the fudge's carefully, plot some data, compare to old, etc.
- Now...Dec 1, 2008 and I'm about to go down to Magellan for the (first?)
radial velocity run. I'd like to include the Smarts 1.3-m data! I modified
the y4k scripts to "andi": andiphot, andiphotit, andicharacter6d, etc. I
ran "andiphot" on the entire set, and then "andiclean" to put them in
subdirectories. Now I need to create new master lists, and I need to do so
right now....
- I **think** this is easy. First, I found images with reasonable seeing
for each cluster. 2007 11/04 was a nice night.
- N346: nrccd071104.0035.fits
- R136: nrccd071104.0047.fits
- N1910: nrccd071104.0041.fits
- N2044: nrccd071104.0046.fits
- N2074: nrccd071104.0065.fits
- I used the original Smarts masterlists as the coordinate sources: fields 5-6 MasterList > cluster.cat and then used mkgsctab to create an table with a name like nrccd071104.0035.fits.tab (oh, Rob!). Got tiny residuals (0.05").
- So, this should be easy, right? wcsctran to find the x and y from the old masterlist...
- fields nrccd071104.0035SUM 1,2,3,6 > SumMaster
- run makenewm.f
- mv fort.4 Masterlist
- matchxy3
- starbyandi
- This produced files with names like N346andi0149, all in their own little
subdirectories. Then what?
- Moved all of the pre-andi files to /users/massey/results/preandi
- Moved all of the andi files to /users/massey/results/andi
- Ran remergem from /users/massey/results
- Moved all of the files to final
- Ran aov on only the stars we cared about. Note that crreject is aliased to crrejectnocn12, which gets rid of that one troublesome Swope night.
Finding Eclipsing Systems from Our Data
How do we identify eclipsing binaries? Last summer undergraduate Erin Roye and I developed software to go through the photometry of each star and note variables. The criteria included
- The 'Classic' E/I test. The "external" error "E" (simply the standard deviation of the magnitudes for a particular star) is compare to the "internal" error "I". The later consists of two components: the instrumental magnitude, and the zero-point uncertainty, added in quadature. The zero-point uncertainty we adopt is 0.02 mag, based upon the dispersion we measured for most stars.
- The maximum minus minimum magnitude divided by the interal error (MaxV-MinV)/I
- The modal value minus the mean value compared to the internal error (V_mode-V_mean)/I.
- Finally, the number of 3-sigma outlyers compared to how many we expect on statistical grounds.
The problem is that none of these criteria work at detecting low-amplitude systems, such as R136-007, where the aplitudes are extremely low, such as in this example:
 The "external" error (standard deviation of all
the photometry) is only 0.03 mag. So, E/I=1.6, if I assume 0.02 mag for
the internal error. The latter is reasonable, as the internal error
is more than just the statistical uncertainty
of the observation, since the zero-points are adjusted for each image.
The "external" error (standard deviation of all
the photometry) is only 0.03 mag. So, E/I=1.6, if I assume 0.02 mag for
the internal error. The latter is reasonable, as the internal error
is more than just the statistical uncertainty
of the observation, since the zero-points are adjusted for each image.
An alternative way is to make use of the additional information that eclipses will be periodic, and so to look only for PERIODIC light variations. Mercedes Lopez-Morales argued this in her thesis analysis of a very large data set (looking for low-mass eclipsing systems, and the demonstrations she makes are quite convincing: see Lopez-Morales & Clemens 2004 PASP, 116, 22. She adopted the Schwarzenberg-Czerny (1989 MNRAS 241, 153) "analysis of variance" (AOV) code to produce periodgrams of star. Ones that show statistically significant spikes are probably winners. I've tried this on the first set of 50 R136 stars, and the results were quite interesting: the KNOWN eclipsing systems pop while most just show noise. One useful diaognostic is that we see harmonics of the correct period. Thus in a frequency periodogram if we see a statistically significant spike at frequence nu, and another spike at 2*nu, we might be suspicious that we have a winner.
Here are some examples:
(1) R136-007.
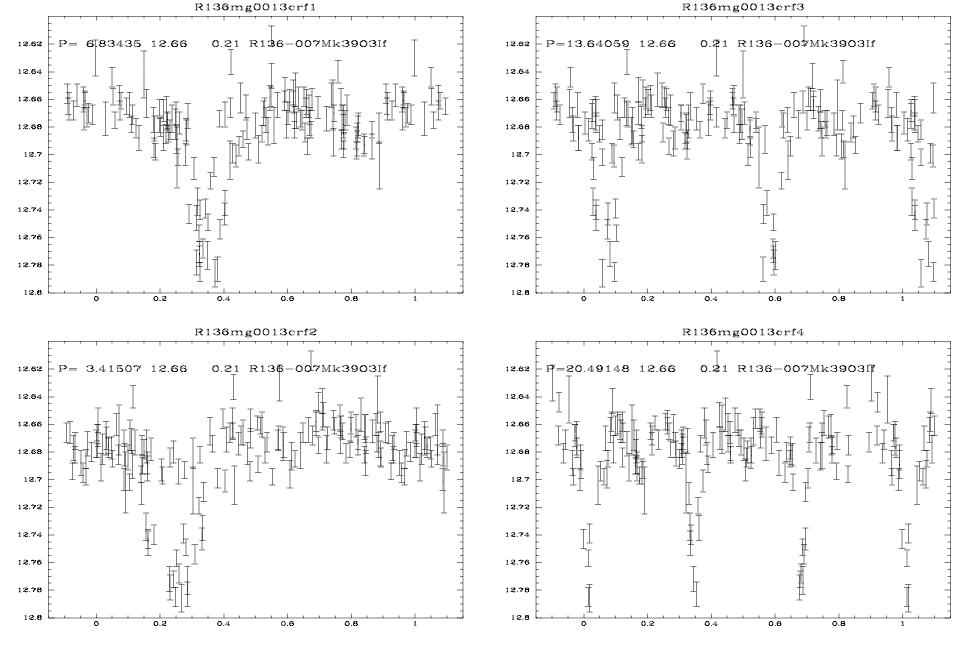
We've know for some time that the period is about 6.8 days. In the periodogram, the fact this is periodic light variable is immediately obvious: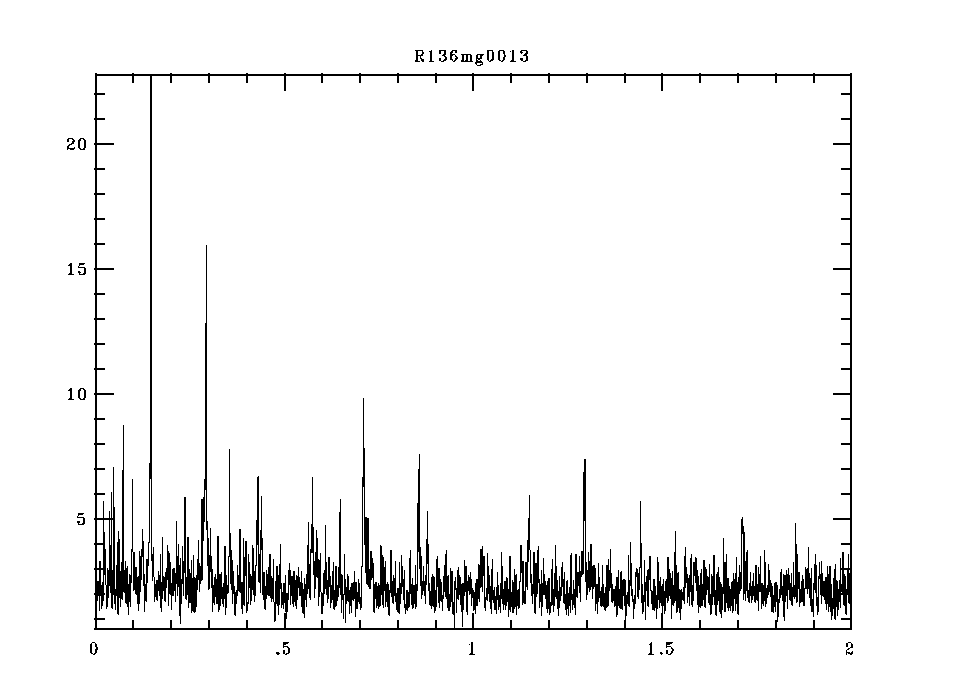
The two largest spikes occur at frequencies of 0.146320 days^-1 (=6.8344 days) and 0.29282 days^-1 (=3.4151 days), where the centers have been determined by the centroid of the three highest points on a spike. So, we suspect that the period is 6.834 days. A Lafler-Kinman search between periods of 1-30 days on the same data yields a best period of 6.8282 days. We would never know this even WAS a light-variable if we were relying upon E/I or other criteria that did not take advantage of the periodic nature.
(2) R136-025.
Previously our "best guess" period was 1.807 days, and the light curve did look like it was in contact (see our NOAO proposal). The AOV periodogram looks like this: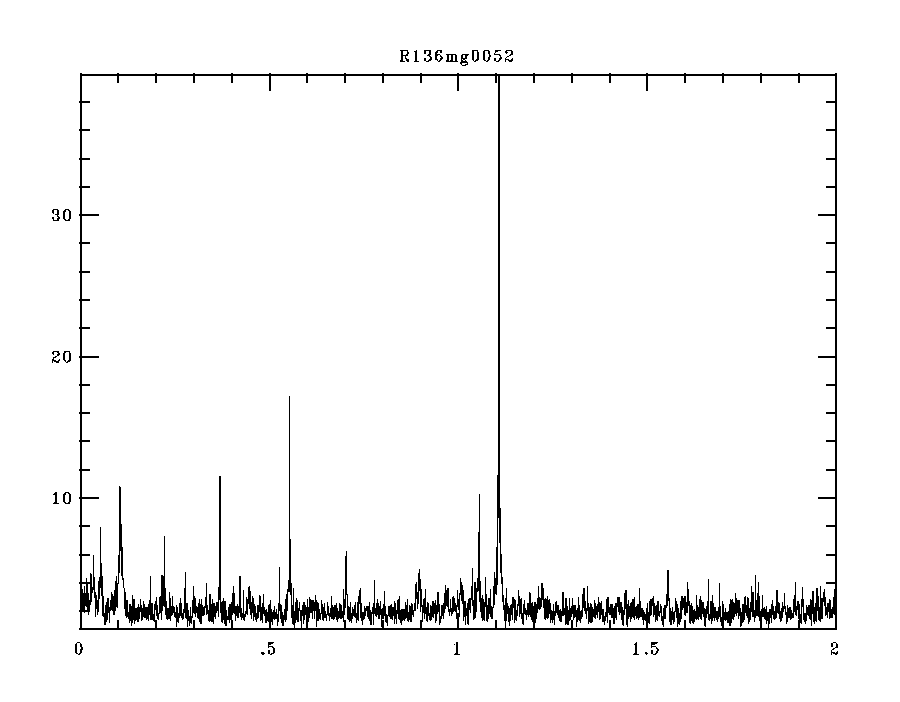
The two strongest spikes occur at 0.55369 days^-1 (1.80606 days), and 1.10730 days^-1 (0.9031 days), again differing by a factor of 2. A Lafler-Kinman search on the same data comes up with a period of 1.806 days.
(3) What about the imfamous case of R136-008?
Our STIS data showed a smooth photometric variation with a period of maybe 25 days: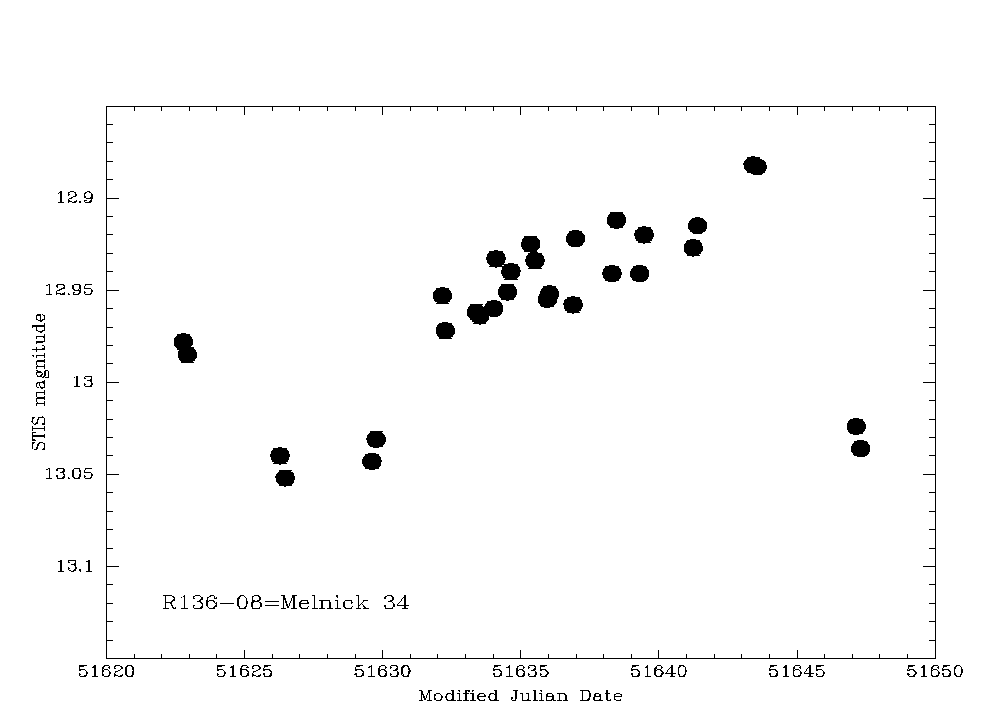
But using only the first set of Swope data I thought I found a nice eclipse with a period of 31.6 days. What does the periodogram show? Not a thing!:
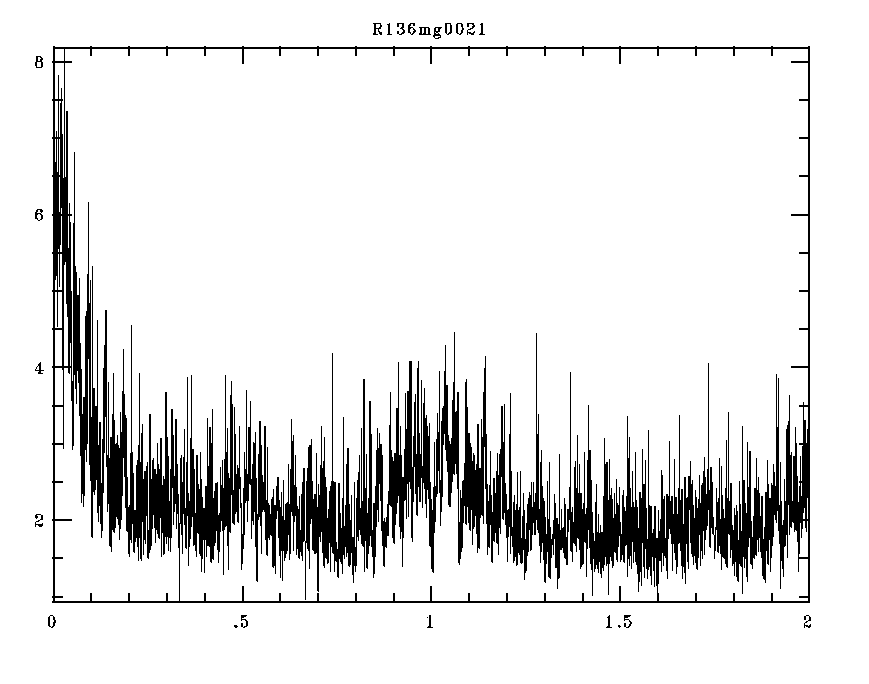
I don't think this is an eclipsing system.
(4) R136-038.
This is the most massive O-type binary known, and was found and analyzed by Massey, Penny, & Vukovich (2002 ApJ, 565, 982) The period we found there was 3.39 days. Its E/I value is 1.3, and the total external error is 0.07 mag. Here's what its periodogram looks like: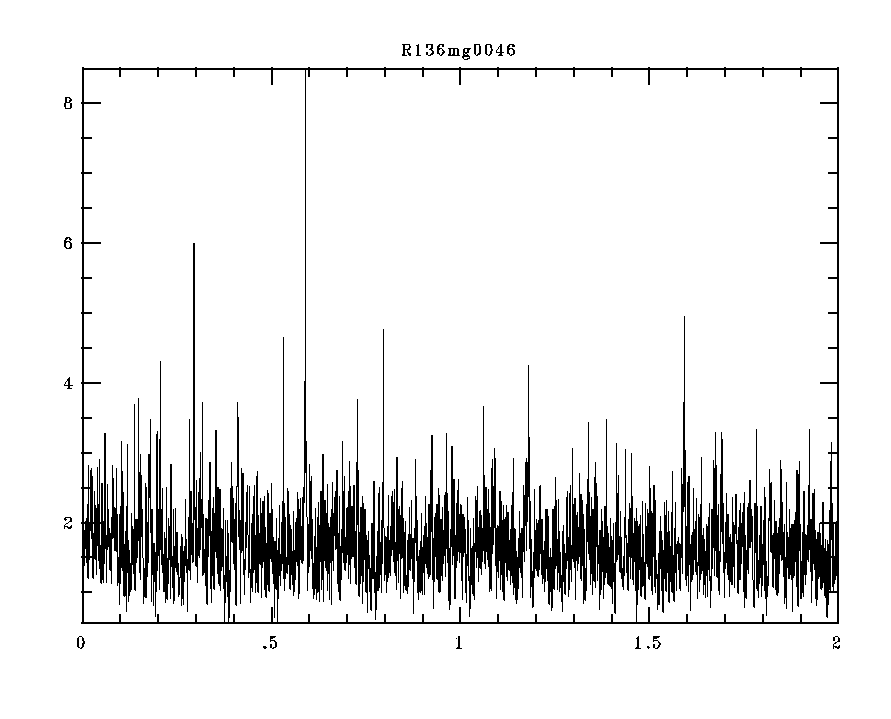
Again, the two largest spikes happen to have a ratio of 2, with frequencies of 0.29507 days^-1 (3.389 days, same as what we found in our published paper) and 0.5903 days^-1 (1.6940 days). A Lafler-Kinman search fails to find any period!
(5) What about some losers?
Here's a typical example, the star R136-028 (O3V):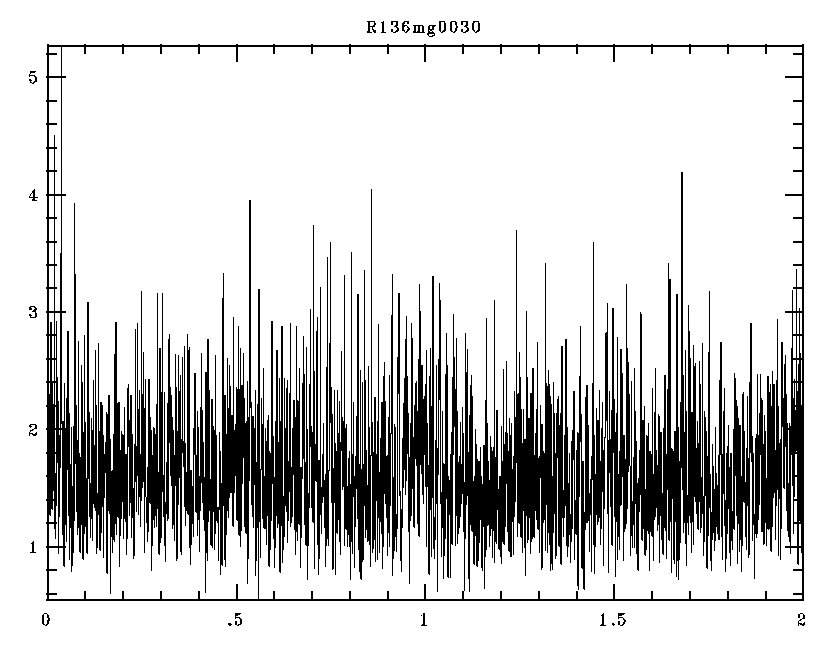
Of course, now the trick is to do this for about 10,000 stars....
Automation
All automation programs feed off the "allstars" file
- Step 1 was to change the delta frequence interveral in "raov" to 1e-5.
Consider observations spanning C days. If we want the phase to drift by
no more than 0.005 phase (say), how well do we need to know the period?
- (C/P)=number of cycles
- Dp=Delta period
- P = period
(C/P) * Dp/P = 0.005, or Dp/P^2 = 0.005 / C.
In frequence space, this is actually easier to consider. How well do we need to know nu? dnu = 1/P^2 dP, and so dnu = 0.005 / C. C is roughly 600 days, so...dnu = 8e-6. Call it 1e-5. But, that means we raov now geneates a STARNAME.res file containing 200,000 points, not 4000!
- The next setp is to automatically look for the most significant spikes. Wrote "findper", which finds the best 5 peaks (if any) from each *.res file. Generates a file STARNAME.per
- autophase generates a phase file for each of those periods. The files are called STARNAME1.pha, STARNAME2.pha, etc.
- makeplots generates an igi plot file for each of those phase files, with names like STARNAME1.com, STARNAME2.com, etc.
- I **think** this is easy. First, I found images with reasonable seeing
for each cluster. 2007 11/04 was a nice night.
I packaged these all together in "period.cl", which also executes the
igi files and generates IRAF "metacode" that can be examined with
gkimosaic. Here's a sample output:
This material is based upon work supported by the National Science Foundation under Grant No. 0506577. Any opinions, findings and conclusions or recommendations expressed in this material are those of the author and do not necessarily reflect the views of the National Science Foundation (NSF).