The Solar-Stellar Spectrograph

[ Home | About | Tech Info & Data | Publications | References ]      [ Site by Jeffrey Hall | Research funded by NSF ]

Ca II H&K absolute intensities and spectrum stacks

This set of articles picks up where the data reduction articles left off.

Our first step in analyzing the data is to place our Ca II H&K spectra on an absolute intensity scale. In the final step of data reduction, we set two points of the HK spectrum to an intensity of 1.0, but that is not the correct value. Due to the heavy obscuration of the spectrum by spectral lines, these two points actually lie somewhat lower, and the exact value will vary depending on the temperature of the star. In this first step of the data analysis, we scale the spectra down to their true intensity values.

The true continuum in the HK order

Once the HK data are normalized to unity, we need to carry out one further normalization step to place the HK spectra on an absolute intensity scale. We do this in several steps.

1. Rebin the 512 pixel HK spectrum to a synthetic high-resolution (~0.02 Å) 5120 pixel spectrum using IDL's Rebin function.

2. Shift the spectra to place all spectral lines at their rest wavelengths.

3. Scale the spectra to the true absolute intensities.

4. Extract parts of all the spectra for a given star and store them in a single "stack" file.

The heart of this procedure is step 3, which sets the spectra up for generating accurate HK indices. We presented the basic method we use in Hall & Lockwood (1995).     
"The Solar-Stellar Spectrograph: Project Description, Data Calibration, and Initial Results." ApJ, 438, 404. [The first major paper from the SSS project.] We use the absolute intensity values at two points (3912 Å and 4000 Å), determined as a log-linear function of stellar color, and then scale the unity-normalized spectrum by a linear fit to the true intensities at these two points. Figure 1 shows the graphical output of our routine SSS::make_stellar_hkstack, which (1) performes this renormalization and (2) compiles all the data from four specific bandpasses in the HK order into spectrum stacks for a given star.

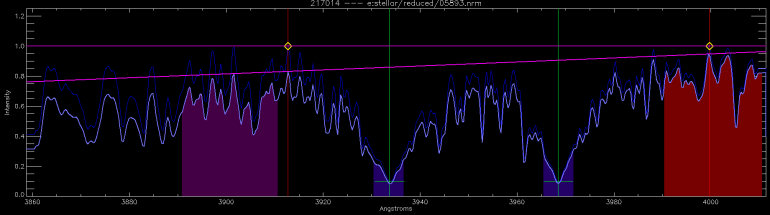
Fig. 1. Scaling the Ca II H&K data to an absolute intensity scale. We begin with the dark blue spectrum (nomalized to unity) and end up with the light blue one (on the true intensity scale). See text for explanation.

In Figure 1, the unity-normalized spectrum is plotted in dark blue. Vertical red lines show the two continuum fitting points, and the green lines show the H and K line centers. The yellow diamonds are the initial values of the pseudocontinuum points the method finds; these should be 1.0 since they are the ones used by the normalizer during data reduction. However, sometimes there are small deviations, so we first calculate a fit to these two points (the dark purple line). It should be a straight line at 1.0, and if it is not, we can flag the spectrum as bad data.

We then calculate the equivalent linear fit to the absolute intensities of the fitting points. This fit is a linear function of B-V valid for for Sun-like (~F-K) dwarfs, and results in the sloping pink line in Figure 1. The final computation is simply S = S / ( f1 / f2 ), where S is the spectrum and f1 and f2 are the fits to the unity points and the absolute intensities, respectively. The end product is the absolutely scaled, light blue spectrum in Figure 1.

The red and purple ranges in Figure 1 are reference bandpasses that correspond precisely to the R and V bands of the Mount Wilson HK photometers. The blue ranges at the H and K line cores span 6 Å centered on the lines; this is to give enough spectrum in the extracted stacks to inspect the inner line wings and account for any systematic drifts. With the four stacks extracted, we can determine the H and K indices (and associated quantities) directly, and we can also calculate a Mount Wilson S as a consistency check.

Procedure

Rebinning spectra to high resolution

To perform subsequent steps in this procedure accurately, we can either use fractional pixels and interpolate on the fly, or simply rebin the data at the outset. It's computationally less burdensome to do this up front, so we use the IDL Rebin function to create high-resolution synthetic spectra with 5120 pixels across the order rather than 512. IDL uses a bilinear interpolation between pixels by default, and this recovers the smoothly varying spectrum precisely; overplots of the original and high-res synthetic spectra are indistinguishable.

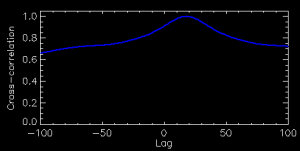
Fig. 2. A representative plot of the cross correlation between a stellar spectrum and the reference solar spectrum for various lags. We shift each spectrum by the lag at the peak of the cross correlation to remove velocity shifts.

Zeroing in velocity

To ensure the HK lines lie at their rest wavelengths, we zero the velocity of the spectrum by cross-correlating it with a reference solar spectrum. The target spectrum is shifted by the requisite number of pixels to move all the spectral features to their rest wavelengths. This is shown in Figure 2. We test the correlation at lags of -100 to +100 pixels from the reference solar spectrum (using the rebinned spectra, which corresponds to +/- 10 pixels in the original spectra). As Figure 2 shows, for the spectrum under consideration the lag peak was +20. This corresponds to ~2 pixels in the original spectrum (a plausible ~50 km/s), and we simply shift the target spectrum by -20 pixels to place it at zero velocity. We use nearly the entire order for calculating the correlation, which makes it quite robust (due to the large number of features for the cross correlation to grab hold of).

Scaling the zeroed spectrum to absolute intensity

This step is described in the description of Figure 1 above. It is the only part of this procedure that alters the data values. There are several ways to check the validity of the scaling. One is to see if the scaled solar spectra match the degraded high resolution atlases; they do, to very good accuracy. Measurement of the total line blanketing can be checked against blanketing reported in other sources. And finally, if we have done things correctly, we should get good agreement between our measures values of Mount Wilson S and the original MWO values, especially for flat activity stars. We will demonstrate the validity of our scaling by all of these methods in subsequent articles.

Spectrum stacks

It is time-consuming and CPU-expensive to read hundreds (or thousands) of spectra from disk every time we want to make an HK time series, so our routine also extracts the parts of the spectrum shown in colored blocks in Figure 1 and combines every observation into a stack file for a given star. I.e., if we have 350 observations of a star, we get four files with data arrays of dimensions [ X, 350 ], where X is the number of pixels in the wavelength range being extracted. With these files in place, subsequent analysis routines need only to open and read the stack files to have every observation of star available in completely uniform arrays.

[Back to contents]