Results of the Solar Disk-center
Spectral Intensity Measurements in the Range 310--1070 nm
K. A. Burlov-Vasiljev, Yu. B. Matvejev, & I. E. Vasiljeva
Main Astronomical Observatory of the National Academy of the
Sciences
Goloseevo, 252650 Kiev-22, Ukraine
burlov@mao.kiev.ua
Abstract
At the high-altitude station on the Peak Terskol (Central Caucasus, 3100 m
a.l.s.) by the Main astronomical observatory of the National Academy of the
Sciences of the Ukraine the spectral measurements of the solar disk-center
intensity have been realized. Data published earlier (1995, Solar Phys.
157, 51) for near UV and visible range are now expanded on the
longwave spectral region up to 1070 nm. The measurements are fulfilled with
the specialized solar telescope. The method of of the solar disk-center
brightness comparison with the brightness of the calibrated reference
ribbon tungsten lamp was used. The atmosphere extinction was taken into
account by Bouger's method with the parallel independent control of the
atmosphere stability. The 1-nm integrals of the disk-center intensity in
range 310---1070 nm now is available. The uncertainty of these values is
estimated by 2%. In the regions with strong telluric absorption by oxygen
and water vapour the supplementary reductions was interred, which was
obtained from the synthetic atmosphere absorption spectra computed on the
basis of molecular parameter atlas HITRAN and standard model of the
atmosphere. With the help of solar disk darkening coefficients the values
of the solar flux at 1 AU are derived. The comparison of the obtained data
with the data by Neckel and Labs (1984, Solar Phys. 90, 205) is
fulfilled as well as with the some other data. From the high-resolution FTS
solar spectrum calibrated with our data we derived the solar continuum
absolute location, which has proved more smooth than the continuum given
by Neckel and Labs. Taking into account our previous measurements in
the near UV and visible, we have compared the results of the solar and
stellar spectro- and multicolor photometry in order to derive the most
exactly adjusted data for solar spectral energy distribution, spectral
energy distribution of Vega, and solar color-indices.
1. Objectives
- Last direct measurements of the absolute solar spectral radiation in
wide UV, visible and IR region were performed at the beginning of 1960 (Labs
and Neckel, Thekaekara et al., Arvesen et al.).
- The previous investigations fulfilled at the Peak Terskol have shown
that the main uncertainties of our ground-based measurements were because
of the uncertainty of standard radiation sources calibration, not
because of the atmosphere extinction reduction procedure.
- The space platform oriented measurements has faced with the
sufficient difficulties of calibration.
- The calibration for the ground-based measurements can be fulfilled
much more precisely and reliably than for the space-based ones.
2. Summary
- The spectral radiation data (disk-center intensity, irradiance at the
1 AU and continuum radiation temperatures) are now available for
the 310---1070 nm wavelength range.
- Figure 1 shows the measured spectral (continuum + lines)
intensity of the solar disk-center radiation in 1012 W m-3 ster-1.
The dotted curve corresponds the data given by Neckel
and Labs.
- Figure 2 shows the disk-center radiation temperatures for local
maxima at 1-nm bands of the calibrated FTS Kitt Peak spectrum. Because of
our integrals are free from atmosphere absorption but FTS spectrum is not,
the telluric lines deviate up from continuum level while the
solar lines deviate down. The continuum is located at the
intervals free from the solar and telluric lines. Dashed line marks the
data by Neckel and Labs, diamonds represent our results.
- The synthetic color-indices of the Sun are very close to
U-B=0.10, B-V=0.62, which are in the high accordance with the data for
the normal G2V star. These values are in the contradiction with the
measured by Tug and Schmidt-Kaler ones (0.18 and 0.67). The synthetic
value V=-26.73 is close to the commonly used -26.75.
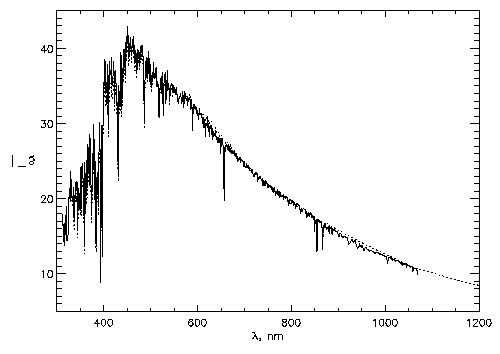
FIGURE 1:Spectral
intensity of the solar disk-center radiation in 1012
W m-3 ster-1 versus wavelength in nm. Thewavelength range
645---685 is the common for both series of the
measurements (UV and visible, 1989: Burlov-Vasiljev et al., 1995;
IR, 1992: Burlov-Vasiljev et al., 1997). The dotted curve corresponds
to the data given by Neckel and Labs (1984).
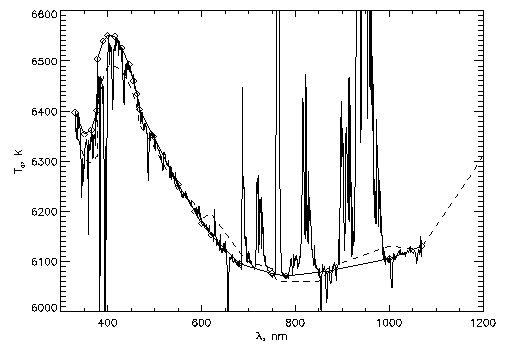
FIGURE 2:Disk-center
radiation temperatures for local maxima at 1-nm bands of the
calibrated FTS Kitt Peak spectrum, continuum of Neckel and Labs (1984)
(dashed line), our results (diamonds). See explanations in
Summary section.
3. Apparatus
The instrumentation adapted for quasi-simultaneous registration of the
solar and standard ribbon tungsten lamp spectra was described by
Burlov-Vasiljev et al.} (1995). It has been installed at Peak Terscol
(Central Caucasus, 3100 m a.l.s.) and consists of:
- solar horizontal telescope with coelostat group (main mirror
D = 230 mm, f = 3 m)
- grating spectrophotometer with collimator (D =
180 mm, f = 2 m), camera mirror (D = 230 mm, f = 2 m), and grating
(140x150 mm, 600 or 1200 grooves/mm) mounted in the vertical
plane. The exit slit, quartz field lens and receiver (photodiode) are mounted
on the scanning carriage, which is moved within 60 mm from the central
point by a stepping motor. For the division of the diffraction orders and
decreasing of the scattered light level the proper colored glasses is
mounted just behind the entrance slit of the spectrometer.
- absolute calibration system uses a ribbon tungsten lamp, which
is placed at the focus of the collimating mirror (D = 230 mm, f = 3 m).
Then the parallel beam is directed to the coelostat mirror and then along
the same optical path as during observations of the Sun. The ribbon lamp
was calibrated in units of the absolute spectral brightness
- atmosphere halo photometer is used for monitoring of the optical
properties of the Earth's atmosphere
- auxiliary equipment to control the apparatus includes optical and
electronical stuff for lamps feeding and control, for the investigations of
the polarization properties of the coelostat group and spectrograph,
for the measurements of spectral reflectivity of the lamp's collimator, etc.
4. Observations
Atmospheric extinction was taken into account by a Bouger's method.
Therefore the procedure of measurements represents the repeated scanning of
an elected area of a spectrum during a day at various air mass in a
direction on the Sun. Usually the air masses were limited by a range
1.2---5.0. The measurements of a solar spectrum were accompanied by
parallel measurements of the solar aureole brightness for a control of
optical stability of the atmosphere. Before fulfillment the day program of
the solar radiation observations the spectrum of the standard lamp in the
same area was measured. Thus the image of the ribbon of the standard lamp
was formed on the entrance slit of the spectrometer with the help of the
spherical collimator mirror.
The two main series of measurements were carried out: for the wavelength range
310---685 nm (1989) and for the wavelength range 645---1070 nm (1992). The
result of 1989 was derived from measurements during 7 days in UV region
(310---400 nm) and 9 days in visible (400---685 nm) during the period
July---August. Totally during 1992 were conducted 3 series of observations
(March 24---April 7, August 4---8, September 29---October 1). All together
there are 19 days of observations. For final result in IR were used the
observations on April 2, 3, 6, 7 and October 1. All the days in March, on
April 1 and on September 29, 30 were extracted because of unsatisfactory
stability of the atmospheric transparency.
The investigated spectral area was divided into few areas, each of which was
measured at a certain position of the diffraction grating. The adjacent areas
were overlapped among themselves on 1/2 length.
5. Calibration
The absolute scale was supported with the help of two tungsten lamps (type
TRU 1100-2350 #359 and #92) with 2x1 mm calibrated area on the
ribbon. They were calibrated as radiance standards at the State Institute
of Optical and Physical Measurements (Moscow, Russia). The accuracy of
calibration was stated as 2.5% at lambda = 300 nm and 1% at lambda
= 1100 nm.
During 1989---1990 years we had conducted numerous comparisons of our lamps
with the standards of some other laboratories of former Soviet Union and
with the standard of the PMOD/WRC (Davos, Switzerland). These measurements
showed that during this period of several years (namely from the moment of
the first calibration in 1988) the lamps saved the brightness within the
limits of a parts of a percent.
The lamps were calibrated in 1988, 1989 and 1990. The differences between
calibrations were within the accuracy bar stated above. During measurements
of a the solar spectrum the lamps were used in different modes. The lamp
#359 was used for calibration daily. The lamp #92 was used not so often --
only for mutual comparisons with the lamp #359 in the very beginning and at
the end of a series of observations. In result the time of burning of a
lamp #92 is less in factor 10 than for a lamp #359. We believe that in this
case the constancy of the ratio of two lamps brightness can be a criterion
of preservation of an internal laboratory scale of measurements. It is very
difficult to assume that both lamps will in coordination change the
brightness at so different modes of use.
The measurements 1992 and result of calibration 1990 differ not more, than
on 1%. We believe, that the scale of our measurements was constant within
that limit.
6. Sources of Uncertainty
We have paid attention to the following possible sources of the
measurements' uncertainty:
- Uncertainty of the lamp's collimator reflectivity.
For the forming of the image of a calibrated area of a lamp ribbon was used
the spherical collimator mirror. Factor of reflection of the mirror was
defined experimentally. Uncertainty of these measurement equals to 1% at
lambda = 300 nm, 0.3---0.5% at wavelengths 400---700 nm, and 1% at
lambda = 1200 nm.
- Transmittance changes of the optical system.
The telescope transmittance changes during the day due to reflectivity
changes of the coelostat mirror with the angle of incidence of the solar
beam. Moreover, the light reflected by the coelostat is partially
polarized, and the amount and character of polarization depends on the
incidence angle. All of the following optical elements are sensitive to
polarization. Thus their transmittance changes during measurements. It
should be noted that the mirror reflectivity is influenced by dust: the
decrease of reflectivity with an increase of incidence angle becomes more
steep. The results of the special investigation can be summarized follows:
- 1. degree of linear polarization after the coelostat mirrors may change
by 1---5% during the day
- 2. polarization properties of the whole spectrometer are mainly due to
the grating
- 3. absorption caused by dust increases by 0.5% with increasing angle
of incidence from 0° to 40°, but influence of the dust upon the
polarization properties is almost zero.
The maximum error caused by variation of the optical system transmittance
can amount to 3%. But this error can be reduced substantially by choosing
the coelostat position and time interval. By this means and with the use of
grating with a small polarization effect, the uncertainty can be
reduced to 0.1---0.2%.
- Detector's stability between calibrations.
It was monitored by radioluminiscent emitters. Trend did not exceed
0.1---0.2% during several hours and the reproducibility is within the
errors of measurements (about 0.2%).
- Detector's linearity.}
Because of differences of solar and lamp brightness, which is up to 4 order
near lambda = 300 nm, detector must have a high linearity. That is why
we used silicon photodiode (spectral sensitivity ranges from 190 to 1100
nm).It was investigated with a set of neutral density filters calibrated at
the State Optical Institute (St. Peterburg, Russia). Results demonstrated a
high linearity over four orders of magnitude.
- Lamp adjustment and feeding.
The transfer of the lamp calibration to the spectrometer is influenced by
the following factors: accuracy of the lamp adjustment inhomogeneity across
the ribbon surface, stability of the power supply, anisotropy of the
radiation and possible temperature effects. Our measurements have shown
that the resulting uncertainty is about 0.5% at lambda = 300 nm and
0.2% at lambda = 1100 nm.
7. Extrapolation to Zero Air Mass
Reduction to zero air mass was fulfilled by the Bouger's method with the
independent monitoring of the atmosphere optical stability (with the help
of the halo photometer and pressure control). For the ``best'' day
the formal uncertainty of the extrapolated to zero air mass solar
disk-center intensity Ilambda,0 is about 0.3% (outside the
molecular absorption bands). For the ``worst'' day adopted for the data
evaluation this value is 1.5%. We have considered the following
restrictions of the Bouger's method:
- Monochromatic radiation.
In UV region the observations were performed with a resolution of 0.5 nm,
and 0.1 nm in visible and IR. The error of the extrapolation to zero air
mass because of nonmonochromatic radiation observed in UV and visible for
these cases is less then 0.2%, but in some narrow regions of the strong
oxygen and water vapour telluric bands in IR it can be extremely large:
for wavelengths 890---990 nm (H2O) - up to 30% (for real water
abundance at Peak Terskol); for wavelengths 759---771 nm (O2) -
75%! In the regions with the strong telluric bands we had to do the added
reduction which was derived from the synthetic atmospheric absorption
spectra computed on the basis of HITRAN molecular parameters data and
standard model of the atmosphere. The uncertainty of these reductions
needed in a few narrow bands is about few percent.
- Accuracy of the air mass computation.
Usually the air mass of Bemporad is used. Straightforward analysis shows
that Bemporad's air mass at some wavelength in UV (with telluric ozone
bands) and IR (water vapour bands) even for observations with zenith
distances less then 75° may cause a relative error in the atmosphere
transparency coefficient of about 3%. We performed a more elaborate
calculation of air mass using real model of atmosphere over Peak Terskol
and taken into account the dependence of air mass on lambda because of
different contribution of Rayleigh scattering, telluric bands and aerosol
extinction to air mass value at different lambda. Obtained values is
valid to within 0.1% for zenith distance less 80°.
- Stable optical atmospheric conditions.
Instability of atmospheric extinction in wide wavelength range is mainly
due to variations of the aerosol portion of the atmosphere. Moreover,
special investigation fulfilled for Peak Terskol show that the atmospheric
water vapour abundance is correlated with abundance of the scattering
aerosol while the absorbing aerosol over Peak Terskol is mostly
absent at all. For monitoring of the scattering aerosol stability we
used atmosphere halo brightness measurements, which let us to find time with
stable atmospheric transparency. As a rule it was only from sunrise to
10-11h of local time.
- Absence of the scattered atmospheric radiation.
Multiple scattering of the light in the atmosphere would affect on the
results obtained with Bouger's method at the high values of the atmospheric
optical thickness (in strong telluric bands only at high air masses). We
have carryed out the model computations to avoid the observations at these
conditions.
8. Results



FIGURE 3:Disk-center
radiation temperatures for local maxima at 1-nm bands of the
calibrated FTS Kitt Peak spectrum, continuum of Neckel and Labs (1984)
(dashed line), our results (diamonds). See explanations in
Summary section.
9. Synthetic UBV
As the solar spectral irradiance data are available for the near UV,
visible and IR range, we can compute the solar color-indices. Here we
presents the results for UBV system.
Different determinations give the value of 0.14---0.20 for (U - B)sun,
and 0.63---0.69 for (B - V)sun (Makarova et al. (1991)). The
values (U - B)sun = 0.18 and (B - V)sun = 0.67 are adopted. These
values differ from the standard meanings for G2V star (0.10 and 0.62
respectively) and are more close G5V (0.20 and 0.68). The absolute
magnitude of the Sun Vsun = -26.70 now is commonly used.
To compute the solar color-indices and absolute magnitude we used the
relative reaction curves for UBV system given by Buser (1978) calibrated
us by spectral energy distribution for Vega. We consider here the following
data set for Vega: by Hayes (1985), Archarov et al. (1989), Terez
(1983), Knyazeva and Kharitonov (1988). In the case of necessary the absent
data at 300 nm was added.
U-B
| Vega calibration | Sun (Neckel & Labs) | Sun (Marakarova et al.) | Sun (Present Work) | Sun (Thekaekara)
| | Knyazeva & Kharitonov | 0.1608 | 0.1770 | 0.1454 | 0.0944
|
| Terez | 0.0798 | 0.0961 | 0.0645 | 0.0134
|
| Archarov et al. | 0.1204 | 0.1367 | 0.1051 | 0.0540
|
| Hayes | 0.1024 | 0.1187 | 0.0871 | 0.0360
|
B-V
| Vega calibration | Sun (Neckel & Labs) | Sun (Marakarova et al.) | Sun (Present Work) | Sun (Thekaekara)
| | Knyazeva & Kharitonov | 0.6318 | 0.5893 | 0.6008 | 0.5645
|
| Terez | 0.6583 | 0.6158 | 0.6273 | 0.5911
|
| Archarov et al. | 0.6461 | 0.6036 | 0.6151 | 0.5789
|
| Hayes | 0.6767 | 0.6342 | 0.6457 | 0.6095
|
V
| Vega calibration | Sun (Neckel & Labs) | Sun (Marakarova et al.) | Sun (Present Work) | Sun (Thekaekara)
| | Knyazeva & Kharitonov | -26.7453 | -26.7291 | -26.7483 | -26.6787
|
| Terez | -26.7469 | -26.7307 | -26.7499 | -26.6803
|
| Archarov et al. | -26.6710 | -26.6548 | -26.6740 | -26.6044
|
| Hayes | -26.7462 | -26.7300 | -26.7491 | -26.6795
|
One can see that the values of the color-indices more close to G5V star are
in the contradiction with the solar and star absolute spectrophotometry.
Moreover, as the both of the color-indices are not independent, they
must lie on the normal stars Main Sequence in the two colors UBV diagram
We could find two close pairs of the spectrophotometer curves for the Sun
and Vega, respectively (present work --- Archarov et
al.), and (Makarova et al. --- Terez), which satisfy
this requirement. In both cases the solar color-indices are typical for G2V
star. The solar absolute magnitude Vsun obtained from
spectrophotometry is close to the commonly-used value.
References
Archarov A.A. et al. 1989, Tables of Standard Reference
Data. Spectral density of energetic illumination from stars on the boundary
atmosphere Earth at the range 0,32...1.08 mcm, GSSSD, Moskow (in Russian).
Arvesen,J.C., Griffin,R.N., & Pearson,B.D. 1969, Appl. Optics.
8, 2215.
Burlov-Vasiljev,K.A., Gurtovenko,E.A., & Matvejev,Yu.B. 1995,
Solar Phys. 157, 51.
Burlov-Vasiljev,K.A., Vasiljeva,I.E., & Matvejev,Yu.B. 1997,
Solar Phys. (in press)
Buser,R. 1978, A&A 62, 411.
Hayes,D.S. 1985, in Hayes,D.(eds.), Calibration of fundamental
stellar quantities, IAU symp. 111, p. 225.
Knyazeva,L.N. & Kharitonov,A.V. 1988, Standard star News.
13, 22.
Lockwood,G.W., T\"ug,H., & WhiteN.M. 1992, ApJ,
390, 668.
Makarova,E.A., Kharitonov,A.V., & Kazachevskaya,T.V. 1991,
Solar Flux, Nauka, Moskow (in Russian).
Neckel,D. & Labs,H. 1984, Solar Phys. 95, 229.
Shaw,G.E. 1982, Appl. Optics. 21, 2006.
Shaw,G.E. & Frö hlich,C. 1979, in B.McCormac and B.Seliga(eds.),
Solar-Terrestrial Influences on Weather and Climate,
D.Reidel Publ. Co., Dordrecht, Holland, p. 69.
Terez,E.I. 1983, Standard star News. 2, 10.
Thekaekara,M.P. 1974, Appl. Optics. 13, 518.
[Contents]





